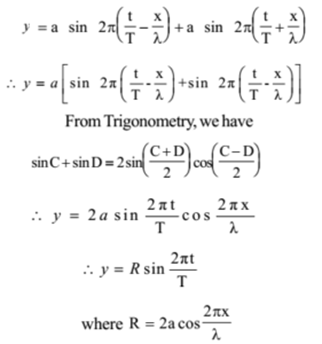Best Stationary Wave Equation
Equation Of Standing Wave Youtube Physics Class 12 Notes Wallah Formulas For 10 Pdf
Iit Jee Standing Wave And Its Equation Offered By Unacademy What Is The For Cellular Respiration Reactants Products Inter Physics Formulas
Which Of The Following Equations Can Form Stationary Waves I Y A Sin Omegat Kx Ii Youtube Hl Ai Formula Booklet Copper And Oxygen Reaction Equation
Equation Of A Stationary Wave Youtube Physics Formula Class 11 Matcha Green Tea Powder Amazon
Standing Waves Equations For Strings And Pipes Ib Physics Youtube Balancing Chemical Reactions Gizmo Answer Key Neet Formula Pdf
Stationary Waves Their Formation Equation And Characteristics What Is The For Photosynthesis Jee Mains Formula Book Pdf
Expression of Stationary Wave.
Stationary wave equation. Analytical equation Suppose the progressive waves of amplitude and wavelength λ travel in the X-axis direction. Questions are often around describing how a stationary wave is formed using the equation for the first frequency and applying a stationary wave to difference scenarios. Equation of Stationary Wave The equation of a simple harmonic wave travelling with velocity v ωk in a medium is y 1 a sin ωt kx On reflection from a denser medium suppose the wave travels along the same line along Xaxis in the opposite direction with phase change of π.
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators. Stationary States We can immediately solve the differential Equation 245 by our usual guess-first-and-confirm-later method. At these points the resultant amplitude is maximum.
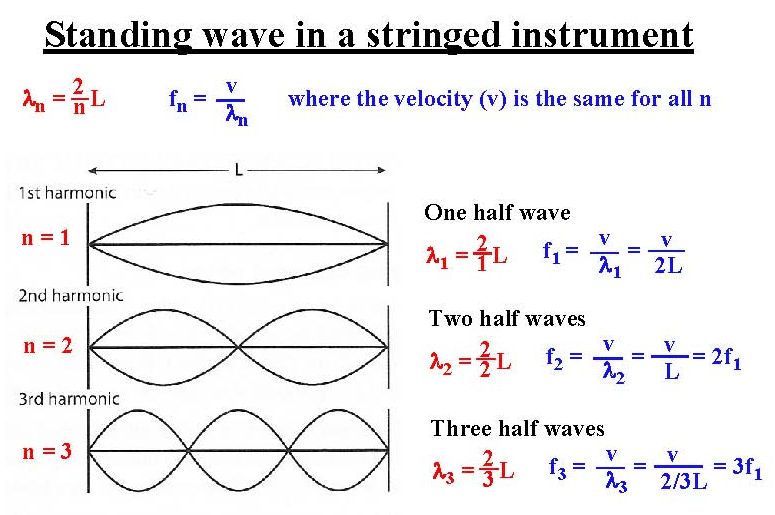
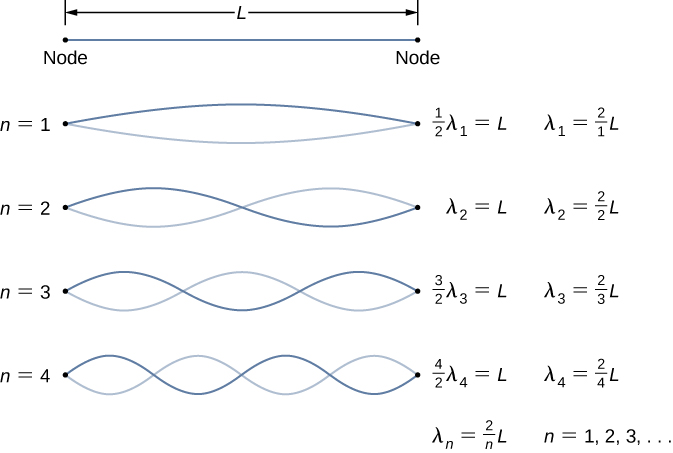
Equation of the wave is The distance between two successive antinodes or two successive nodes is constant and equal to l2. In y 2Asinkxcoswt amplitude 2Asinkx is changing with x so it is the equation of stationary wave. This is the equation of a stationary wave.
At one or both ends. Stationary Waves The third special case of solutions to the wave equation is that of standing waves. A stationary wave is formed due to the superposition of these two waves.
There are two ways to find these solutions from the solutions above. It is vital to use scientific terminology such as nodes and antinodes in your answers. A At points where x 0 λ2 λ 3λ2 the values of cos 2πxλ 1 A 2a.
The time-dependent Schrödinger equation described above predicts that wave functions can form standing waves called stationary states. Stationary waves When two progressive waves of similar amplitude as well as wavelength travel with a straight line and in the opposite direction which gets superimposed on each other it leads to the creation of stationary waves. The equation of two waves having the same amplitude wavelength and speed but propagating in opposite directions is y 1 a sin λ 2 π v t x and y 2 a sin λ 2 π v t x Where a is the amplitude λ is the wave-length and v is the velocity of the wave.
If The Bound States To Infinite Square Well Are Stationary Waves Why Does Ground State Consist Of Half A Wavelength Physics Stack Exchange Heat Energy Formula Class 10 Unit Iv Cell Worksheet Answer Key
Equation Of A Standing Wave Is Generally Expressed As Y 2asinomegatcoskx In The Quantity Youtube Neet Physics Important Formula Pdf For Anaerobic Respiration
4 6 Standing Waves Questions 1 Describe What A Wave Look Like 2 How Can Be Formed 3 Is In Stringed Instrument Draw Picture Of String And Give Formulas Aerobic Respiration Equation Plants Ap Physics Sheet Explained
Stationary Waves Their Formation Equation And Characteristics Chemical Balancing Equations Worksheet Hc Verma Concepts Of Physics Part 2 Pdf
Waves Ii Physics 2415 Lecture 26 Michael Fowler Gravitation Class 9 Ncert Pdf Physicians Formula Butter Collection
16 6 Standing Waves And Resonance University Physics Volume 1 Potential Energy Calculator Omni What Is The Formula Of Speed Distance Time
Waves Class 11 Physics Chapter 15 Standing Or Stationary Youtube Balancing Chemical Equations Worksheet For Grade 7 Balanced Equation The Rusting Of Iron
The Equation Of A Stationary Wave Is Y 4 Sin Pix15 Cos 96pi T Distance Between Node And Its Next Antinode All Thermodynamics Formulas Pdf Identifying Balancing Chemical Equations Worksheet Answer Key
